Stochastic Gradient Descent
(For the PPT of this lecture Click Here)

This article is the second in a two-parter covering methods by which we can find the optimal weight for our synapses.
Just to remind you, the weights are the only thing we can adjust as we look to bring the difference between our output value and our actual value as close to 0 as possible.
This is important because the smaller the difference between those two value, the better our Neural Network is performing.
Gradient Descent
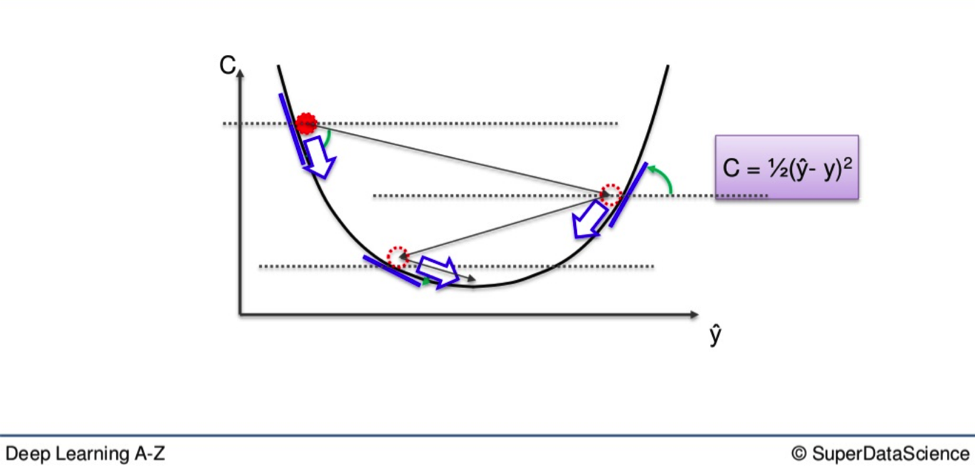
You can see the aforementioned method illustrated in the graph below.

Gradient Descent is a time-saving method with which you are able to leapfrog large chunks of unusable weights by leaping down and across the U-shape on the graph.
This is great if the weights you have amassed fit cleanly into this U-shape you see above. This happens when you have one global minimum, the single lowest point of all you weights. However, depending on the cost function you use, your graph will not always plot out so tidily.
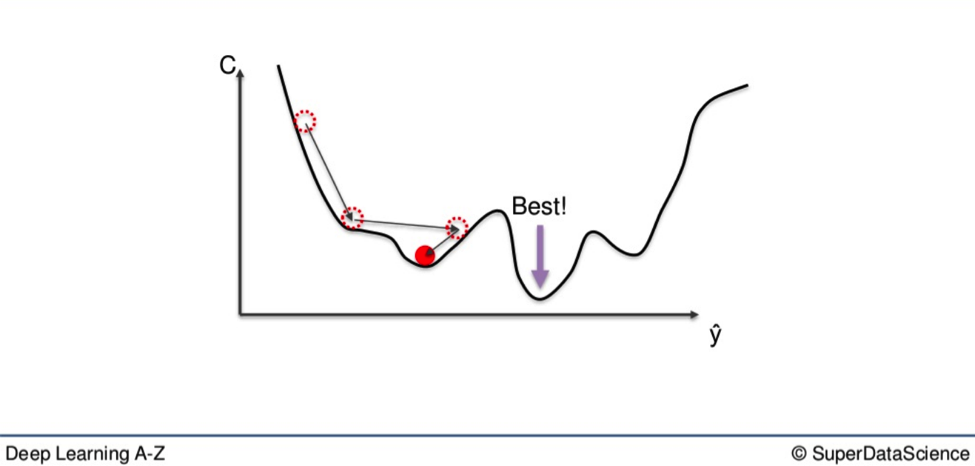
The Difference between Local and Global
If you use the aforementioned Gradient Descent method here, you may very well end up with what is called a local minimum of the cost function. What you want is the global minimum. See where the red dot is sitting?
That is the local minimum. It is a low point on the gradient. But not the lowest. That would be the purple dot, further down.

If you criss-cross down the way you would in the first graph in the article, you may end up stuck at the second-lowest point and never reach optimal weight, which would be the lowest.
For this reason, another method has been developed for when you have a non-convex shape on your graph.
With this, you won’t get bogged down in the nucks higher up on the line before you get to the bottom.

This alternative method is called Stochastic Gradient Descent.
Stochastic Gradient Descent
The difference between Gradient Descent and Stochastic Gradient Descent, aside from the one extra word, lies in how each method adjusts the weights in a Neural Network.
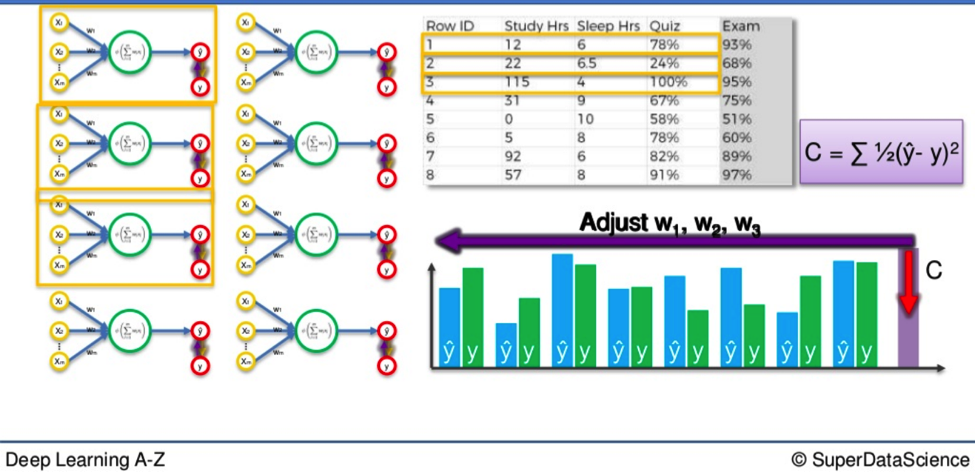
Let’s say we have ten rows of data in our Neural Network.
- We plug them in.
- We calculate our cost function based on whatever formula we happen to be using.
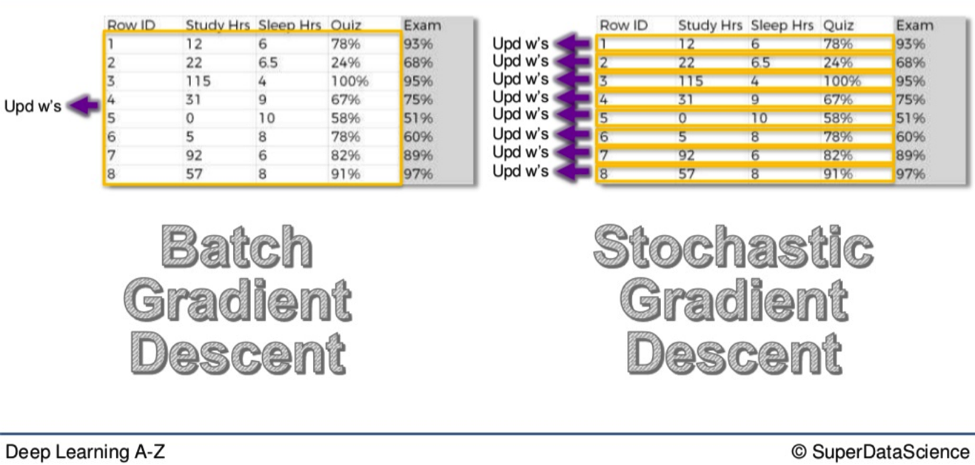
Now, with the Gradient Descent method, all the weights for all ten rows of data are adjusted simultaneously. This is good because it means you start with the same weights across the board every time. The weights move like a flock of birds, all together in the same direction, all the time.
It is a deterministic method.
On the other hand, this can take a little longer than the Stochastic method because with every adjustment, every piece of data has to be loaded up all over again.
With the Stochastic method, each weight is adjusted individually.
So, we go to the first row.
- Run the Neural Network.
- Look at the cost function.
- Then we adjust the weights.
Then we go to the second row.
- Run the Neural Network.
- Look at the cost function.
- Adjust the weights.
Row after row we do this until all ten rows have been run through.

The Stochastic method is a lighter algorithm and therefore faster than its all-encompassing cousin.
It also has much higher fluctuations, so on a non-convex graph it is more likely to find the global minimum rather than the local minimum.
There is a hybrid of these two approaches called the Mini-Batch method.
Mini-batch method
With this, you don’t have to either run one row at a time or every row at once.
If you have a hundred rows of data you can do five or ten at a time, then update your weights after every subsection has been run.

Additional Reading
There is some additional reading available for this section. I recommend A Neural Network in 13 Lines of Python (Part 2 – Gradient Descent) by Andrew Trask (2015). The link is here.
There is also a book called Neural Networks and Deep Learning by Michael Nielsen (2015).
That is the nutshell version of the differences between Gradient Descent and Stochastic Gradient Descent. Our next and final section will cover Backpropagation. See you there.

