Gradient Descent
(For the PPT of this lecture Click Here)


This is a continuation of the last deep learning section on how Neural Networks learn. If you recall, we summed up the learning process for Neural Networks by focusing on one particular area.
Reducing the Cost Function
The cost function is the difference between the output value produced at the end of the Network and the actual value. The closer these two values, the more accurate our Network, and the happier we are. How do we reduce the cost function?
Backpropagation
This is when you feed the end data back through the Neural Network and then adjust the weighted synapses between the input value and the neuron.
By repeating this cycle and adjusting the weights accordingly, you reduce the cost function.
How do we adjust the weighted synapses?
In the last article, I pointed out that the weights are the only thing within our Network that we can tamper with. Throughout the rest of the process, the Network is essentially operating independently.
This puts all the more emphasis on how and why we alter the weights.
If you make the wrong alteration it would be like having a car with the front axle pointing slightly to the left, and while you are driving you to let go of the steering wheel but keep your foot on the gas.
Sooner or later, you’re going to crash.

Two ways to adjust the weights
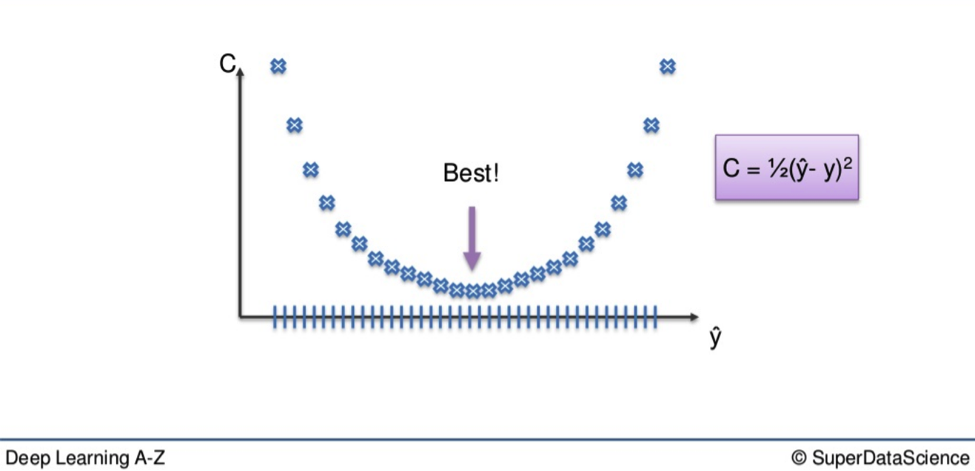
The first is the brute-force approach. This is far better suited to a single-layer feet-forward network. Here you take a number of possible weights. On a graph it looks like this:

You can see there are a number of blue dots. As we have already established, we want to lower the cost function i.e. reduce the difference between our output value and actual values.
We want to eliminate all other weights except for the one right at the bottom of the U-shape, the one closest to 0.
The closer to 0, the lower the difference between output value and actual value.
That is where we find our optimal weight.
You could find your way to the best weight through a simple process of elimination. You could trial every weight through your network and one-by-one get closer and closer to your optimal weight. On a simple level, this would suffice, say if you only had a single weight to optimize. But the larger a network becomes, the number of weights that will emerge means this method is impracticable.
You could have an almost infinite amount of weights to adjust. Therefore a process of elimination would be like looking for the prettiest grain of sand on a beach. Good luck with that.
This problem is known as the Curse of Dimensionality.
To put a mind-bending timescale on it, an advanced supercomputer would need a longer time than the universe has existed to find all the optimal weights in a mildly complex Neural Network, when using this process of elimination. Obviously, that won’t do.
Gradient Descent

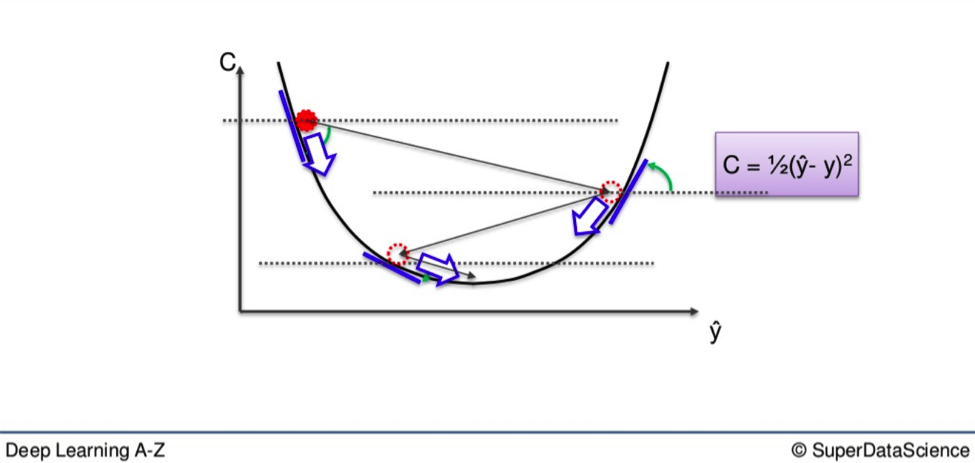
Here you see how gradient descent works in a simple graphic representation.
Instead of going through every weight one at a time, and ticking every wrong weight off as you go, you instead look at the angle of the cost function line.
If the slope is negative, like it is from the highest red dot on the above line, that means you must go downhill from there.
For the sake of remembering the journey downwards, you can picture it like the old Prince of Persia video games.

You need to jump across the open space, from ledge to ledge, until you get to the checkpoint at the bottom of the level, which is our 0.
This eliminates a vast number of incorrect weights on the way down. It also reduces the time and effort spent on finding the right weight.
It is a far more efficient method, I’m sure you will agree. That is just an examination of the process in principle. At the end of the next section, I will provide you with some additional reading and there will be further information once we reach the application phase.
Next, we will go into deep learning on Stochastic Gradient Descent. See you there.

